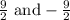We have the equation:
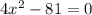
We can see that there is a differnce of squares:
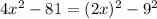
And then we can rewite the difference of squares as:
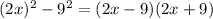
And this is equal to 0:
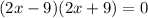
Now, there are two possibilities:
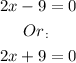
Then, we need to solve this two equatiions:
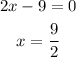
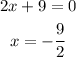
The two solutions for the equation are: