Question

Select the correct choice below and fill in any answer boxes in your choice.

Answer 1

The equation is given to be:

`(x)/(x-9)+2=(9)/(x-9)`

We can simplify the left-hand side of the equation using the LCM method:

`\begin{gathered} (x)/(x-9)+2=(x+2(x-9))/(x-9) \\ =(x+2x-18)/(x-9) \\ =(3x-18)/(x-9) \end{gathered}`

Thus, the equation becomes:

`(3x-18)/(x-9)=(9)/(x-9)\text{ --------(A)}`

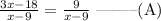
To further simplify, we can multiply both left and right-hand sides of the equation by the common denominator (x - 9). This eliminates the denominator, thus we have:

`\begin{gathered} 3x-18=9 \\ 3x=9+18 \\ 3x=27 \\ \therefore \\ x=(27)/(3) \\ x=9 \end{gathered}`

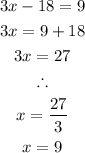
The solution to the equation is 9.

We can confirm the answer by checking for the undefined (singularity) points of the equation.

An equation is undefined if the denominator is equal to 0. The denominator of our equation is

`x-9`

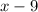
We will equate this to 0 so that we can get a value for x that will make the expression undefined:

`\begin{gathered} x-9=0 \\ x=9 \end{gathered}`

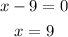
Therefore, we have the undefined point of the equation to be 9.

Since this coincides with our only solution for the equation, this means that 9 cannot be a solution of the equation.

Therefore, THERE IS NO SOLUTION.

OPTION B is correct.