We have to find the representation of the solution set of the inequality:

We can divide this inequality into two, as the absolute value function is like a piecewise function.
We can calculate it in the case that 2x-1 is negative. Then, we can solve it as:

When 2x-1 is positive, we can solve it as:
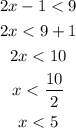
Then, if we combine the two results, the solution set is -4 < x <5 and it represented as Option C.
Answer: Option C.