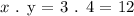Question:
The equations of 2 lines are shown below. 2x - y = 2 3x + 4y = 25 What is the product of (x.y) of the point of intersection?
Solution:
Consider the following line equations:
Equation 1
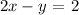
Equation 2:

Now, solving equation 1 and equation 2 for the variable y, we get:
Equation 3:

and
Equation 4:
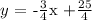
now, if we relate equations 3 and 4 we obtain:
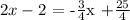
this is equivalent to:

this is equivalent to:
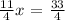
this is equivalent to:
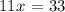
this is equivalent to:
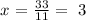
then:
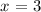
now, replacing this in equation 3, we get:
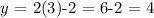
thus

Thus the point of the intersection is (x,y) = (3,4) and we can conclude that the product of x = 3 and y = 4 is :