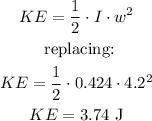Question

Two thin rods of length L are rotating with the same angular speed, W (in rad/s) about axes that pass perpendicularly through one end. Rod A is massless but has particle of mass 0.63 kg attached to its free end. Rod B has mass of 0.63 kg, which is distributed uniformly along its length. The length of each rod is 0.82 m, and the angular speed is 4.2 rad/s. Find the kinetic energies of rod A with its attached particle and of rod B.

Answer 1

Rod A: 3.74 J

Rod B: 3.74 J

Explanation:

Rod A:

Length of the Rod = l = 0.82 m

Mass of particle attached = m = 0.63 kg

Moment of inertia of the system about given axis:

`\begin{gathered} I=m\cdot l^2 \\ \text{ replacing} \\ I=0.63\cdot(0.82)^2 \\ I=0.424\text{ kg}\cdot m^2 \end{gathered}`

Angular speed of the rod = 4.2 rad/s

Kinetic energy of the rod is:

`\begin{gathered} KE=(1)/(2)\cdot I\cdot w^2 \\ \text{ replacing:} \\ KE=(1)/(2)\cdot0.424\cdot4.2^2 \\ KE=3.74\text{ J} \end{gathered}`

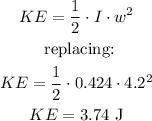
Rod B:

Length of the Rod = l = 0.82 m

Mass of particle attached = m = 0.63 kg

Moment of inertia of the system about given axis:

`\begin{gathered} I=m\cdot l^2 \\ \text{ replacing} \\ I=0.63\cdot(0.82)^2 \\ I=0.424\text{ kg}\cdot m^2 \end{gathered}`

Angular speed of the rod = 4.2 rad/s

Kinetic energy of the rod is:

`\begin{gathered} KE=(1)/(2)\cdot I\cdot w^2 \\ \text{ replacing:} \\ KE=(1)/(2)\cdot0.424\cdot4.2^2 \\ KE=3.74\text{ J} \end{gathered}`