Question

Glven: y varies directly with x and has a constant rate of change of 7. When the value of y is 12, then the value of x would be?

Answer 1

Since y varies directly with x, we will be using this formula:

`\text{ y = kx}`

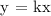
Given:

Constant rate of change = k = 7

Let's substitute k to generate the equation. We get,

`\text{ y = 7x}`

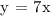
Let's now determine the value of x when y = 12.

`\text{ y = 7x }\rightarrow\text{ x = }(y)/(7)`
`\text{ x = }(12)/(7)`

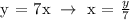
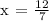
Therefore, at a constant rate of change of 7 and y varies directly with x, a value of y = 12 will have an x value of 12/7.