To obtain the cost of one game system, the following steps are necessary:
Step 1: Let the unknown costs of a game system and a video game be represented by the variables x and y, respectively.
That is :
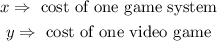
Step 2: Transform each of the first two sentences of the question into mathematical equations, as follows:
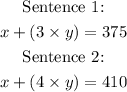
Step 3: Assign the equations numbers, and solve them simultaneously, as below:
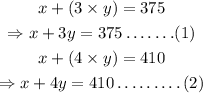
Now:

Finally:
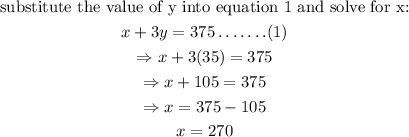
Therefore the cost, in dollars, of one game system is 270