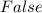Question

Hello I could use help with these two questions thanks i do not understand

Answer 1

Explanation

We are given the following system of equations:

`\begin{gathered} x-y+z=2\text{ \lparen equation 1\rparen} \\ 2x-3y+4z=4\text{ \lparen equation 2\rparen} \\ -3x+4y+z=0\text{ \lparen equation 3\rparen} \end{gathered}`

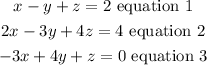
Joe subtracted equation 3 from equation 1 and the result is

`Result:-4x-5y=2`

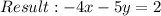
We are required to determine if the result is correct or not.

- Since, equation 3 is subtracted from equation 1, this is written mathematically as:

"Equation 1 - Equation 3"

Therefore, we have:

`\begin{gathered} \text{ Equation 1 - Equation 3} \\ \text{ }x-y+z=2 \\ - \\ \text{ }-3x+4y+z=0 \\ \text{ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_} \\ x-(-3x)-y-(+4y)+z-(+z)=2-0 \\ x+3x-y-4y+z-z=2-0 \\ 4x-5y=2 \\ \\ Note:(-4x-5y=2)\text{ is not }(4x-5y=2) \end{gathered}`

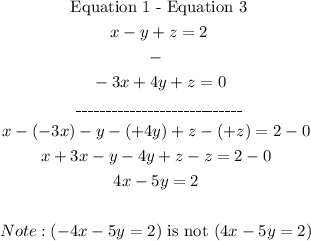
Hence, the answer is:

`False`