Question

A guitar string is 128 cm long and has a mass of 2 g. Knowing that the wave speed in the string is 40 m/s, then the tension, F_T, in the string is

Answer 1

Given:

• Length of string, L = 128 cm

,

• Mass, m = 2 g

,

• Speed, v = 40 m/s

Let's find the tension in the string.

To find the tension in the string, apply the formula:

`v=\sqrt{(T)/(\mu)}`

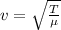
Where:

v is the speed

T is the tension

μ is the linear density.

Rewrite the formula for T:

`T=v^2*\mu`

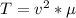
• To solve for μ, we have:

`\mu=(m)/(l)`

Where:

m is the mass (2g) in kg = 2 x 10⁻³ kg

L is the length in meters = 1.28 m

Hence, we have:

`\begin{gathered} \mu=(2*10^(-3))/(1.28) \\ \\ \mu=0.0015625 \end{gathered}`

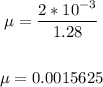
Now, to find the tension, we have:

`\begin{gathered} T=v^2*\mu \\ \\ T=40^2*0.0015625 \\ \\ T=1600*0.0015625 \\ \\ T=2.5\text{ N} \end{gathered}`

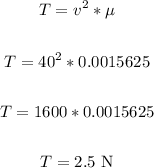
Therefore, the tension in the string is 2.5 N

ANSWER:

2.5 N