Question

The equations of 4 lines are given. Identify which lines are parallel

Answer 1

We are given the equations of four lines and we are asked to determine which ones are parallel. To do that we need to remember that two lines are parallel if they have the same slope. To determine the slope the line equations must be written in the form:

`y=mx+b`

Where "m" is the slope.

The first equation is:

`y=-(3)/(4)x-6`

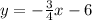
Therefore, the slope of the first equation is:

`m_1=-(3)/(4)`

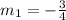
The second equation is:

`y-7=-4(x+9)`

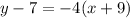
We need to rewrite the equation to the wished form in order to know the slope, therefore we need to solve for "y". We do that first by applying the distributive property on the right sides:

`y-7=-4x-36`

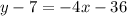
Now we add 7 to both sides:

`\begin{gathered} y=-4x-36+7 \\ y=-4x-29 \end{gathered}`

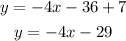
Therefore, the slope of this line is:

`m_2=-4`

For the third equation we have:

`y=-2x+6`

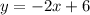
The slope of this equation is:

`m_3=-2`

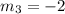
For the fourth equation we have:

`x+(4)/(3)y=-5`

Now we solve for "y", first we subtract "x" from both sides:

`(4)/(3)y=-5-x`

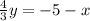
Now we multiply both sides by "3/4":

`y=-(15)/(4)-(3)/(4)x`

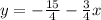
Therefore, the slope of the fourth line is:

`m_4=-(3)/(4)`

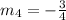
Since we have:

`m_1=m_4`

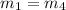
Then lines 1 and 4 are parallel.