Question

The distribution of heights of adult men in the U.S. is approximately normal with mean 69 inches and standard deviation 2.5 inches. Use what you know about a normal distribution and the 68-95-99.7 rule to answer the following. (a) About what percent of men are between 69 and 74 inches? (b) About 2.5 percent of all men are shorter than?(c) About what percent of men are between 64 and 66.5 inches?

Answer 1

The 68-95-99.7 rule let us draw some conclusions about a normally distributed population, knowing only the mean and standard deviation.

For example, 68% of the data falls within one standard deviation from the mean. In this case, with mean 69 and standard deviation of 2.5, 68% of the data is between 69-2.5=66.5 and 69+2.5=71.5.

The same can be written for 95% and 2 standards deviation from the mean and 99.7% and 3 standard deviations from the mean.

(a) We have to calculate what percent of men are between 69 and 74.

69 is the mean and 74 is 2 times the standard deviation from the mean:

`(74-\mu)/(\sigma)=(74-69)/(2.5)=(5)/(2.5)=2`

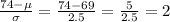
For 74, we apply the 95% rule, but split in half, as we are measuring from the mean and not -2 standard deviation.

The percent of men between 69 and 74 is 95%/2 = 47.5%.

Answer: 47.5%.

b) We have to find the height for which only 2.5% of the men are below.

To calculate this we can use the 95% rule, for which we know that 2.5% of the data are in each of the tails.

Then, we know that the shorter 2.5% is below a height that is equal to the mean less 2 times the standard deviation.

`H=\mu-2\sigma=69-2\cdot2.5=69-5=64`

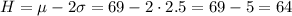
Then, 2.5% of the men are shorter than 64 inches.

Answer: 64 in.

c) The percent of men that are between 64 (2 times the standard deviation below the mean) and 66.5 (one time the standard deviation below the mean) can be calculated using both the 68% rule and the 95% rule.

We know that 47.5% of the data is between 64 and 69 (half of 95%).

We also know that 34% of the data is between 66.5 and 69 (half of 68%).

Then, between 64 and 66.5 there is 47.5%-34%=13.5% of the data.

The percent of men that are between 64 and 66.5 inches is expected to be 13.5%.

Answer: 13.5%.