The best way to answer this question would be to try out the choices that are available. Use the choices to find the value of y for each value of x.
Let's try the first one.
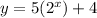
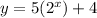
Let's solve for y when x = -2.
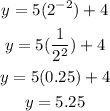
Because y = 5.25 and not 2.25 when we use the first equation, then that option is wrong. Let's try the second one.
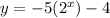
Again, when x = -2,
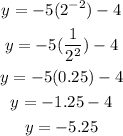
The answer is -5.25, which means this option is also wrong. Let's try the third one.
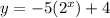

Because the y-value is 2.75, we can try out the other values of x to make sure that it is also correct when the values of x are changed.
For x = -1:
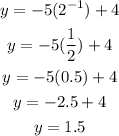
For x = 0:

Foor x = 1:

We see that for almost all of the values of x, the y-values are the same as those given in the table. Since we have tried 4 points already, it is safe to assume that the third option is the correct answer.
The answer is y = -5(2^x)+4.