Question

I need some help, having two units of ft and two angles is giving me some difficulty with knowing how to apply the trig identities

Answer 1

We will start from the top

We have a small right triangle with an angle of measure 30 degrees

and hypotenuse of length 30 feet

We will use the sine ratio to find its horizontal side which is a part of d

`\sin (30)=(d1)/(30)`

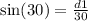
By using cross multiplication

`\begin{gathered} d1=30\sin (30) \\ d1=15 \end{gathered}`

Now we will work on the triangle which has an angle of measure 75 degrees

and the length of its hypotenuse is 200 feet

We will use the cosine ratio because d is adjacent to the angle of 75

`\cos (75)=(d-d1)/(200)`

By using cross multiplication

`d-15=200\cos (75)`

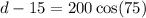
Add 15 to both sides to find d

`\begin{gathered} d=15+200\cos (75) \\ d=66.76380902 \end{gathered}`

The distance d = 66.76 feet