For h=0.1 the difference quotient of the given function is:
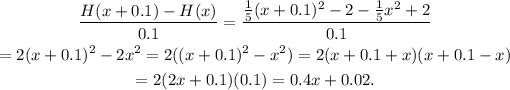
For h=0.01 the difference quotient of the given function is:
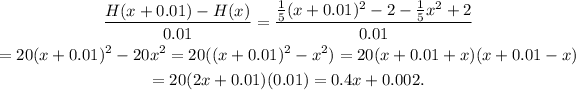
For h= 0.001 the difference quotient of the given function is:
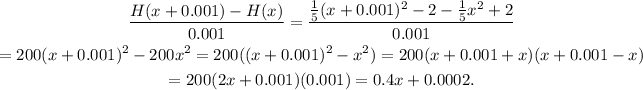
Substituting x= 5 in each quotient we get:
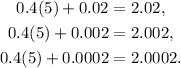
Answer:
Slope of the tangent line: 2.