Question

Write the proportional equation for the table that represents a proportional relationship. Use the variable that is provided in parenthesis beside each label.

Answer 1

The proportional relationship can be express as y = kx, where x is the independent variable and y is the dependent variable.

For table 1, T is the independent variable and C is the dependent variable, so the relationship that we are looking for is C = kT

Using the table, C = 30 when T = 2.

Substitute this to find k.

`\begin{gathered} C=kT \\ 30=2k \\ k=(30)/(2)=15 \end{gathered}`

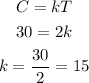
Therefore, the equation is C = 15T

For table 2, G is the independent variable and C is the dependent variable. So the equation is C = kG

Using the table, C = 10.60 when G = 4.

Substitute this to find k.

`\begin{gathered} C=kG \\ 10.60=4k \\ k=(10.60)/(4)=2.65 \end{gathered}`

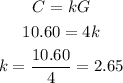
The equation is C = 2.65G