Question

Suppose 4.14 g of H2 S04 was needed to neutralize 85.00 mL of NaOH. What was the molarity of the base? The molar mass of H2SO4 is 98.09g/mol 2NaOH(aq)+H2SO4(aq)=Na2SO4(aq)+2 H2O(I)

Answer 1

Let's find the number of moles of 4.14 g of H2SO4 using its molar mass:

`4.14gH_2SO_4\cdot\frac{1molH_2SO_4}{98.09\text{ }gH_2SO_4}=0.042\text{ mol }H_2SO_4\text{.}`

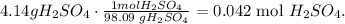
With this value, we can calculate how many moles of NaOH (base) we have to calculate its molarity. In the chemical reaction, you can see that 2 moles of NaOH react with 1 mol of H2SO4, so doing a rule of three:

`\begin{gathered} 2\text{ moles NaOH}\to1\text{ mol }H_2SO_4 \\ \text{? moles NaOH}\to0.042\text{ moles }H_2SO_4\text{.} \end{gathered}`

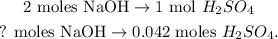
And the calculation would be:

`0.04\text{2 moles }H_2SO_4\cdot\frac{2\text{ moles NaOH}}{1\text{ mol }H_2SO_4}=0.08\text{4 moles NaOH.}`

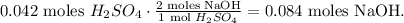
Now we can calculate the molarity using the formula:

`\text{Molarity}=\frac{moles\text{ of solute}}{\text{Volume in liters}}.`

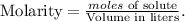
But before doing that, we need to convert 85 mL to liters. Remember that 1 liter equals 1000 mL:

`85.00mL\cdot\frac{1\text{ L}}{1000\text{ mL}}=0.085\text{ L.}`

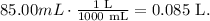
And finally, we can calculate the molarity like this:

`\begin{gathered} \text{Molarity}=\frac{0.084\text{ moles}}{0.085\text{ L}}, \\ \text{Molarity}=0.988\text{ M.} \end{gathered}`

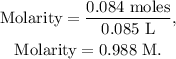
The answer is that the molarity of the base before neutralizing it is 0.988 M.