Question

how a pendulum works including how fast it moves as its wing what happens to its energy as it swings and why it eventually stops.

Answer 1

A simple pendulum is considered to be a point mass suspended from a string or rod of negligible mass. If the pendulum is displaced from its equilibrium position, it will swing due to the force of gravity. Additionally, if there is damping (that can come from friction with the air), the pendulum will loose energy as it swings until it stops moving.

According to the variables in the diagram, the maximum velocity of a pendulum can be calculated using the conservation of mechanical energy:

The height that the mass reaches is equal to:

`h=L(1-\cos \theta_0)`

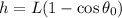
The potential energy at that point, is:

`\begin{gathered} U=mgh \\ =mgL(1-\cos \theta_0) \end{gathered}`

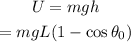
The kinetic energy at the equilibrium position will be related to the maximum velocity:

`K=(1)/(2)mv^2_(\max )`

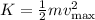
Then:

`\begin{gathered} K=U \\ \Rightarrow(1)/(2)mv^2_(\max )=mgL(1-\cos \theta_0) \\ \end{gathered}`

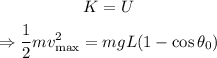
Isolate v_max:

`\begin{gathered} \Rightarrow v^2_(\max )=2gL(1-cos\theta_0) \\ \Rightarrow v_(\max )=\sqrt[]{2gL(1-\cos \theta_0)} \end{gathered}`