Question

What is the value of the section/area A, B? (ft. squared)

Answer 1

Step-by-step explanation:

Given;

We are given a square with two unshaded portions labelled A and B.

Required;

We are required to find the area of the sections A and B.

Step-by-step solution;

To do this, first of all take note that the section labelled A has a side with length 4ft. The other side is also 4 ft. We know this because the corresponding side shows 4ft + 4ft.

This means what we have is a sector of a circle with radius 4ft.

To calculate the area of sector A (and B), we shall apply the formula;

Formula;

`\begin{gathered} Area\text{ }of\text{ }a\text{ }sector: \\ Area=(\theta)/(360)*\pi r^2 \end{gathered}`

Note that the variables are;

`\theta=90\degree,r=4,\pi=3.14`

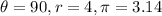
We can now substitute these values and solve;

`Area=(90)/(360)*3.14*4^2`
`Area=(1)/(4)*3.14*16`
`Area=12.56ft^2`

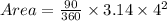
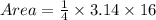
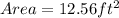
Therefore, the area of the sector A and B are;

ANSWER:

`\begin{gathered} A=12.56ft^2 \\ B=12.56ft^2 \end{gathered}`

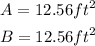
Note that the dimensions are the same for sectors A and B. Hence, the areas are the same for both.