Question

A bank loaned out $18,000 part of it at the rate of 8% per year and the rest at 16% per year. If the interest received in one year total $2500, how much was loaned at 8%? How much of the 18,000 did the bank loan out at 8%?

Answer 1

The Solution:

Given that a bank loaned out $18000.

Let the amount loaned out at 8% per year be represented with x.

So that the amount loaned out at 16% per year will be $(18000-x)

Recall: By formula for simple interest ( since the simple interest is the same as compound interest if the period under consideration is 1 year), we have:

`I=\frac{\text{PRT}}{100}`

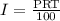
So, for the loan at 8% per year:

`\begin{gathered} I_{1_{}}=\text{ interest=?} \\ P\text{ =principal=\$x} \\ T=\text{ time =1year} \end{gathered}`

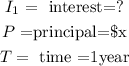
So, for the loan at 16% per year:

`\begin{gathered} I_{2_{}}=\text{ interest=?} \\ P\text{ =principal=\$(18000-x)} \\ T=\text{ time =1year} \end{gathered}`
`(I_1+I_2)=(8* x*1)/(100)+((18000-x)*16*1)/(100)`
`(I_1+I_2)=\text{ \$2500}`
`2500=(8x)/(100)+(16(18000-x))/(100)`
`2500=(8x+288000-16x)/(100)`

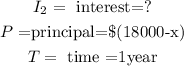
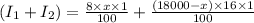
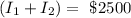
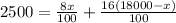
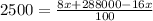
Cross multiplying, we get

`250000=288000-8x`
`\begin{gathered} 8x=288000-250000 \\ 8x=38000 \end{gathered}`

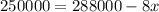
Dividing both sides by 8, we get

`x=(38000)/(8)=\text{ \$4750}`

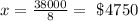
Thus, the amount loaned at 8% is $4750.

Therefore, the correct answer is $4750.