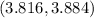Question

According to scientists, the cockroach has had 300 million years to develop a resistance to destruction. In a study conducted by researchers, 4,000 roaches (the expected number in a roach-infested house) werereleased in the test kitchen. One week later, the kitchen was fumigated and 15,400 dead roaches were counted, a gain of 11,400 roaches for the 1-week period. Assume that none of the original roaches died duringthe 1-week period and that the standard deviation of the number of roaches produced por roach in a 1-week period, is 1.3. Use the number of roachos produced by the sample of 4,000 roaches to find a 90%confidence interval for the mean number of roaches produced per week for each roach in a typical roach-infested house.Find a 90% confidence interval for the mean number of roachos produced per week for each roach in a typical roach-infested house,(Round to three decimal places as needed.)

Answer 1

Before working on the answer, let us define some things:

`\begin{gathered} \sigma=1.3 \\ n=4000 \end{gathered}`

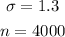
Besides, we need to calculate the average (x bar) of roaches produced by a single roach in the week:

`\bar{x}=(15400)/(4000)=3.85`

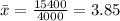
Let's look at our z-score table. the value associated with a confidence level of 90% is

`z^{}=1.645`

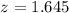
Having calculated these things, we're done; for the desired confidence interval is given by

`CI=(\bar{x}-z\cdot\frac{\sigma}{\sqrt[]{n}},\bar{x}+z\cdot\frac{\sigma}{\sqrt[]{n}})`

Replacing the values we just got:

`CI=(3.85-(1.645)\cdot\frac{1.3}{\sqrt[]{4000}},3.85+(1.645)\cdot\frac{1.3}{\sqrt[]{4000}})\ldots`
`\ldots\approx(3.85-0.0338,3.85+0.0338)=(3.816,3.884)`

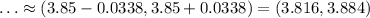
The answer is

`(3.816,3.884)`