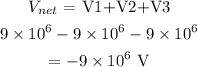Question

Obtain the potential on the x-axis at x = 0 for the following point charge distributions on the x-axis: 200 μC at x = 20 cm, -300 μC at x = 30 cm and -400 μC at x = 40 cm60v,90v,-60v,-90v

Answer 1

Given:

The charge

`\begin{gathered} q1\text{ = 200 }\mu C \\ =200*10^(-6)\text{ C} \end{gathered}`

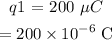
is at a distance x1 = 20 cm = 0.2 m.

The charge

`\begin{gathered} q2\text{ = -300 }\mu C \\ =-300*10^(-6)\text{ C} \end{gathered}`

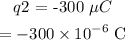
is at a distance x2 = 30 cm = 0.3 m.

The charge

`\begin{gathered} q3\text{ = -400 }\mu C \\ =-400*10^(-6)\text{ C} \end{gathered}`

is at a distance x3 = 40 cm = 0.4 m.

To find the potential at x = 0

Step-by-step explanation:

The potential can be calculated by the formula

`V=(kq)/(x)`

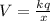
Here k is Coulomb's constant whose value is 9 x 10^(9) Nm^2/C^2

Potential due to charge 1 is

`\begin{gathered} V1\text{ =}(kq1)/(x1) \\ =(9*10^9*200*10^(-6))/(0.2) \\ =9*10^6\text{ V} \end{gathered}`

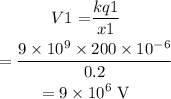
Potential due to charge 2 is

`\begin{gathered} V2\text{ =}(kq2)/(x2) \\ =(9*10^9*-300*10^(-6))/(0.3) \\ =-9*10^6\text{ V} \end{gathered}`

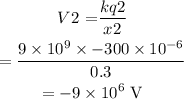
Potential due to charge 3 is

`\begin{gathered} V3\text{ =}(kq3)/(x3) \\ =(9*10^9*-400*10^(-6))/(0.4) \\ =-9*10^6\text{ V} \end{gathered}`

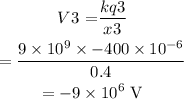
Thus, the net potential at x = 0 is

`\begin{gathered} V_(net)\text{ = V1+V2+V3} \\ 9*10^6-9*10^6-9*10^6 \\ =-9*10^6\text{ V} \end{gathered}`