Question

Solve 67 . Find the equation and also sketch the graph.

Answer 1

An object enters the solar solar system. Also the sun is at the origin of the path.

The equation of the entering object is given as,

`\begin{gathered} y\text{ = }2x\text{ -2 } \\ y\text{ = 2 ( x - 1)} \end{gathered}`

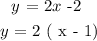
The equation for departing the solar system is given as,

`\begin{gathered} y\text{ = -2x + 2} \\ y\text{ = -2 ( x - 1 )} \end{gathered}`

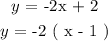
The combined equation for the object is given as,

`y\text{ = }\pm2(x-1)`

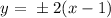
The equation of the asymptote is given as,

`y\text{ = }\pm(b)/(a)(\text{ x -h )+k}`

Comparing the given equation with the asymptote we get,

`\begin{gathered} (b)/(a)\text{ = 2} \\ h\text{ = 1} \\ k\text{ = 0} \end{gathered}`

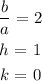
The distance from the sun is 0.5 au .

Therefore,

`\begin{gathered} a\text{ = 0.5} \\ (b)/(0.5)\text{ = 2} \\ b\text{ = 2 }*\text{ 0.5} \\ b\text{ = 1} \end{gathered}`

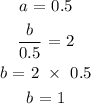
The general equation for the hyperbola symmetric to x axis is given as,

`((x-h)^2)/(a^2)\text{ + }((y-k)^2)/(b^2)\text{ = 1}`

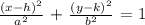
Substituting the given values in the equation ,

a = 0.5 , b = 1 , h = 1 and k = 0.

`\begin{gathered} ((x-1)^2)/(0.5^2)+((y-0)^2)/(1^2)\text{ = 1} \\ ((x-1)^2)/(0.25)+(y^2)/(1^2)\text{ = 1} \\ 4(x-1)^2+y^2\text{ = 1} \end{gathered}`

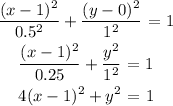
Thus the required equation is ,

`4(x-1)^2+y^2\text{ = 1}`

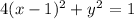
The graph is given as: