Variables
• x: length of one of the pieces, in inches
,
• y: length of the other piece, in inches
The addition of both pieces makes the original rope which is 60 inches long. Then:
x + y = 60 (eq. 1)
If one piece must be twice as long as the other, then:
x = 2y (eq. 2)
Substituting equation 2 into equation 1:
2y + y = 60
Combining similar terms:
3y = 60
Dividing by 3 at both sides of the equation:
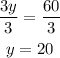
Substituting this result into equation 2:
x = 2y
x = 2*20
x = 40
One of the pieces must be 40 in long and the other one must be 20 in long