Question

Solve the system give ordered pairs16x+3y=1388x+3y=90

Answer 1

`\begin{gathered} 16x+3y=138 \\ 8x+3y=90 \end{gathered}`

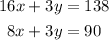
To solve a system of equations you:

1. Solve one of the equations for one of the variables:

Solve x in first variable:

`\begin{gathered} 16x=138-3y \\ \\ x=(138)/(16)-(3)/(16)y \\ \\ x=(69)/(8)-(3)/(16)y \end{gathered}`

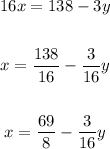
2. Use the value of x you find in part 1 in the second equation:

`8((69)/(8)-(3)/(16)y)+3y=90`

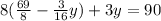
3. Solve for y:

`\begin{gathered} 69-(24)/(16)y+3y=90 \\ \\ -(3)/(2)y+3y=90-69 \\ \\ (-3y+6y)/(2)=21 \\ \\ (3)/(2)y=21 \\ \\ y=21((2)/(3))=(42)/(3)=14 \end{gathered}`

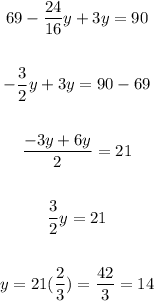
4. Use the value of y to find the value of x:

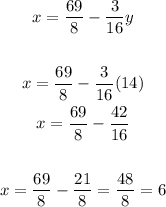
`\begin{gathered} x=(69)/(8)-(3)/(16)y \\ \\ x=(69)/(8)-(3)/(16)(14) \\ x=(69)/(8)-(42)/(16) \\ \\ x=(69)/(8)-(21)/(8)=(48)/(8)=6 \end{gathered}`Then, the solution of the system is ( 6, 14)