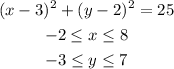1 Answer

Colm Ryan · Answer 1 · 2023-09-26T13:22:40+0000

Given the parametric equations:

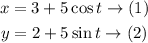
$\begin{gathered} x=3+5\cos t\rightarrow(1) \\ y=2+5\sin t\rightarrow(2) \end{gathered}$

We will use the following equations to eliminate t:

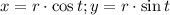
$x=r\cdot\cos t;y=r\cdot\sin t$

So, the given equations will be as follows:

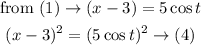
$\begin{gathered} \text{from (1)}\rightarrow(x-3)=5\cos t \\ (x-3)^2=(5\cos t)^2\rightarrow(4) \end{gathered}$

and from equation (2)

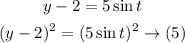
$\begin{gathered} y-2=5\sin t \\ (y-2)^2=(5\sin t)^2\rightarrow(5) \end{gathered}$

Add the equations (4) and (5)

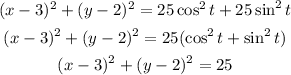
$\begin{gathered} (x-3)^2+(y-2)^2=25\cos ^2t+25\sin ^2t \\ (x-3)^2+(y-2)^2=25(\cos ^2t+\sin ^2t) \\ (x-3)^2+(y-2)^2=25 \end{gathered}$

So, the rectangular equation is a circle with radius = 5 and the center = (3, 2)

So, the answer will be option C:

$\begin{gathered} (x-3)^2+(y-2)^2=25 \\ -2\le x\le8 \\ -3\le y\le7 \end{gathered}$

Please log in or register to add a comment.