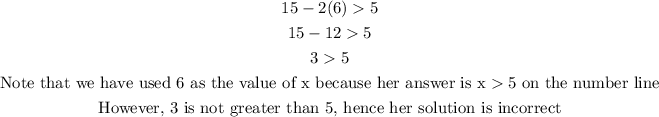Question

Mariah solved the inequality 15-2x>5 and got x>5 as a solution. Describe how you can use a number line to prove that her solution is incorrect.

Answer 1

Solve the inequality;

`\begin{gathered} 15-2x>5 \\ \text{Subtract 15 from both sides of the inequality} \\ 15-15-2x>5-15 \\ -2x>-10 \\ \text{Divide both sides by -2} \\ (-2x)/(-2)<(-10)/(-2) \\ x<5 \end{gathered}`

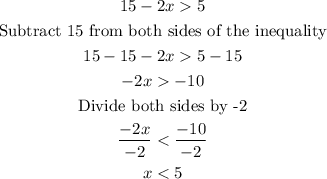
As a rule in math, when an inequality is divided by a negative number, the sign is flipped backwards. This simply means whe dividing by a negative number, the sign "greater than" is flipped back to "less than" and vice versa.

If according to Mariah's solution the answer is x > 5, that means we woud have the following;

`\begin{gathered} 15-2(6)>5 \\ 15-12>5 \\ 3>5 \\ \text{Note that we have used 6 as the value of x because her answer is x}>5\text{ on the number line} \\ \text{However, 3 is not greater than 5, hence her solution is incorrect} \\ \end{gathered}`