Question

1. Find domain of the function, = ln(2 − 6 − 55).

Answer 1

Domain of a function

We want to find the domain of the following function:

`=ln\mleft(^2-6-55\mright)`

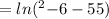
This means that we want to find the x-values that it can take.

STEP 1: analyzing the simplies form of the function

Let's analyze the simpliest form of the function:

`=ln(x)`

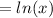
Its graph is:

Then, for the simpliest form of the function, the x-values can only be higher than 0.

This means that its domain is

domain = x > 0

STEP 2: domain of the given function

Based on the above we can deduce that for the ln(x) function, what is inside the parenthesis should be higher than 0 on this kind of functions.

This is that for

`=ln\mleft(^2-6-55\mright)`

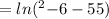
then

`^2-6-55>0`

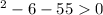
STEP 3: finding the x values that make x²-6x-55>0 (factoring)

In order to find the values of x that make

`^2-6-55>0`

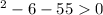
we must factor it.

We want to find a pair of numbers that when multiplied give the last term (-55) and when added together give the second term (-6).

For the last term of the polynomial: -55, we have that

(-5) · 11 = 55

5 · (-11) = 11

If we add them:

-5 + 11 = 6

5 - 11 = -6

The pair of numbers that when multiplied give the last term (-55) and when added together give the second term (-6), are: 5 and -11

We use them to factor the polynomial:

`^2-6-55=(x+5)(x-11)`

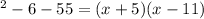
Then,

`(x+5)(x-11)>0`

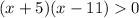
STEP 4: finding the x values that make (x+5)(x-11)>0 (factoring)

In order to find them, we are going to separate the factors (x+5) and (x-11) and analyze when they are positive or negative:

Combining them:

Since we are going to multiply both factors:

`(x+5)(x-11)`

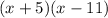
We use the diagram to analyze the sign of their product:

Then

`(x+5)(x-11)>0`

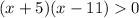
when x < -5 and when x > 11. This is the domain.

Therefore, expressed in set notation:

domain = x∈(-∞, -5)∪(11, ∞)

Answer: domain = x