The price of purchase can be represented as a function of the numbers of shirts bought in a way that the function is linear. This means that it increases at a constant rate. A linear function has the following form:
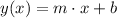
Where m is the rate of change and b is the y-intercept. The rate of change on our case is the price of the shirt and the y-intercept is the one time fee. To determine the value of m we can use the following expression:

Where (x1, y1) and (x2, y2) are points that belong to the line. We will choose the points (5, 55) and (10, 105).

To find b we need to replace one known point on the first expression.
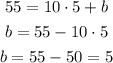
The expression is:
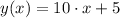
The correct answer is the third one.