1 Answer

Jonathan Works · Answer 1 · 2023-02-10T19:34:18+0000

We start with the function f(x)=x^1/2 and end witht the function g(x)=-2(x-2)^1/2-3.

We have to find the transformations.

The first transformation is a scale with a factor of 2:

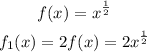
$\begin{gathered} f(x)=x^{(1)/(2)} \\ f_1(x)=2f(x)=2x^{(1)/(2)} \end{gathered}$

The second transformation is a reflection over the horizontal axis:

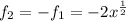
$f_2=-f_1=-2x^{(1)/(2)}$

The third transformation is a translation in the horizontal axis, 2 units to the right. Then, we have:

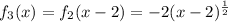
$f_3(x)=f_2(x-2)=-2(x-2)^{(1)/(2)}$

The fourth transformation is a translation 3 units down:

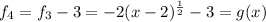
$f_4=f_3-3=-2(x-2)^{(1)/(2)}-3=g(x)$

Answer: The transformation are:

1) Dilation with a scale factor of 2.

2) Reflection over the x-axis.

3) Translation 2 units to the right.

4) Translation 3 units down.

We can sketch the graph of all the transformations as:

Please log in or register to add a comment.