Given the function f(x) = x3 + 5x2 – X – 4, find...
a) f'(-2).
b) the values of a such that f'(a) = 56.
step 1
Find f'(x)
first derivative
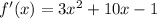
f'(-2)
For x=-2
substitute
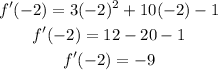
step 2
the values of a such that f'(a) = 56.
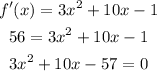
Solve the quadratic equation
solve by using the formula
a=3
b=10
c=-57
substitute
![x=\frac{-10\pm\sqrt[\square]{10^2-4(3)(-57)}}{2(3)}](https://img.qammunity.org/2023/formulas/mathematics/college/4drfhdtwuq3mrpbkp04mwev739q96xwih0.png)
![x=\frac{-10\pm\sqrt[\square]{784}}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/4yh2frg11ndvhage8ykvujehn2m3zw6scd.png)
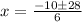
the values of x are
x=3 and x=-19/3