To solve this problem, we will use the following property of exponents:
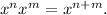
Now, notice that:
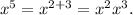
Therefore, we can rewrite the given expression as follows:
![x^2y\sqrt[]{18x^2y^2x^3}.](https://img.qammunity.org/2023/formulas/mathematics/college/vldl5xb7fye1w47kd4bqp3xszdirnkr079.png)
Recall that:
![\sqrt[]{ab}=\sqrt[]{a}\sqrt[]{b}.](https://img.qammunity.org/2023/formulas/mathematics/college/28awd4fvqi6sz9hk7yomqlwmcxdeabdmkk.png)
Therefore, we can split the root as follows:
![x^2y\sqrt[]{18x^2y^2x^3}=x^2y\sqrt[]{18}\sqrt[]{x^2y^2}\sqrt[]{x^3}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/851xwhganu6um5nbh0jnvacjftendkm3ve.png)
Simplifying we get:
![x^2y\sqrt[]{18}\sqrt[]{x^2y^2}\sqrt[]{x^3}=x^2y\sqrt[]{9\cdot2}\sqrt[]{x^2}\sqrt[]{y^2}\sqrt[]{x^3}=x^2y3\sqrt[]{2}xy\sqrt[]{x^2x}.](https://img.qammunity.org/2023/formulas/mathematics/college/vb1bn8uoczqok6etdcvre7fywemqkee5wz.png)
Multiplying like terms, we get:
![x^2yxy\sqrt[]{18x^3}=x^4y^2\sqrt[]{18x}=x^4y^2\sqrt[]{(9\cdot2)x^2}=3x^4y^2\sqrt[]{2x}.](https://img.qammunity.org/2023/formulas/mathematics/college/26dxwqwsa5413qf7zt86p5786p3hca2lf0.png)
Answer:
![3x^4y^2\sqrt[]{2x^3}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/mxvovwd9znf56jdmkijsg8mxaikmnvk8ed.png)
Example:
Simplify
![2x^2y^3\sqrt[]{9x^3y^2}.](https://img.qammunity.org/2023/formulas/mathematics/college/o01gnoc7qq6yar63wki27quxae6k12m01e.png)
First, we notice that:
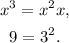
Therefore, we can rewrite the expression as:
![2x^2y^3\sqrt[]{3^2x^2xy^2}=2x^2y^3\sqrt[]{3^2x^2y^2}\sqrt[]{x}=2x^2y^3(3xy)\sqrt[]{x}.](https://img.qammunity.org/2023/formulas/mathematics/college/akcmzugu28j3og3ka2r8hvs69brz7sn0us.png)
Simplifying we get:
![6x^3y^4\sqrt[]{x}.](https://img.qammunity.org/2023/formulas/mathematics/college/jz421dplhyahs55nlb1dvliqblmk6j1ta8.png)