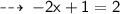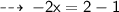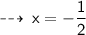Here we go ~
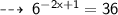
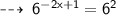
now, let's apply logarithm on both sides with base (6)
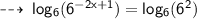
According to properties of logarithm, the exponent on the number come out and it's written as a product of exponent times the logarithm.
that is :
![\sf [ log_(a)(b {}^(n) ) = n * log_( a )(b) ]](https://img.qammunity.org/2023/formulas/mathematics/high-school/ujpx8npjehlsp18a3e9tycydhp5v7rkq1k.png)

now, as we know : when the base and argument of log are same, then value of log is 1