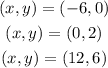Given the linear equation:
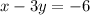
The single linear equation above contains two variables. Hence, there is no unique solution but infinitely many pairs of solutions. For every value of x, there is a value for y.
Three points that solve the equation would be:
Solution 1
Put x = -6 into the equation
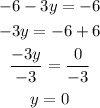
Solution 2
Put x = 0 into the equation
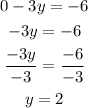
Solution 3
Put x = 12 into the equation
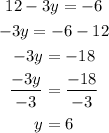
Therefore, three points that solve the linear equation as shown above are: