Step 1: Write out the general equation for a linear function

Step 2: Write out a linear function for the height and the amount of time
If h represents height and t represents time. The equation of the linear function connecting h and t would be
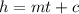
Step 3: Write out the general formula for finding the equation of linear function given two different coordinates
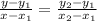
For the function of h and t, the formula would be
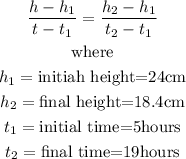
Substitute for the given parameters in the formula
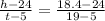
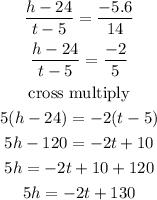
Divide through by 5
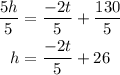
The above function connect the height and the amount of time together
Step 4: Find the height of the candle after 10 hours
![\begin{gathered} \text{When t=10} \\ h=(-2(10))/(5)+26 \\ h=-4+26 \\ h=22\operatorname{cm} \end{gathered}]()
Hence, the height of the candle after 10 hours is 22cm