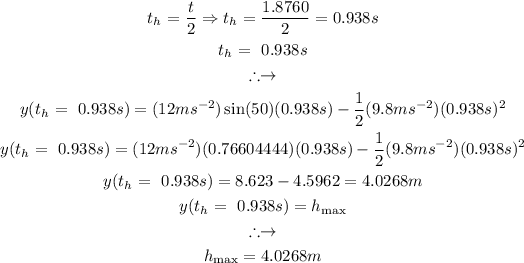Question

A ball is thrown into the air at an angle of 50 from the horizontal with an initial velocity of 12 m/s. Calculate both of the steps in the solution: 1- The time of the ball's flight in the air 2- The maximum height the ball reaches

Answer 1

`\begin{gathered} (1)\Rightarrow t=1.8760 \\ (2)\Rightarrow h_(\max )=4.0268m \\ \end{gathered}`

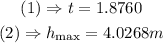
Step-by-step explanation: A ball is thrown into the air at an angle of 50 degrees with a horizontal, and initial velocity of 12m/s. (i) we to find the total time of the flight, and (ii) maximum height that the ball reaches

(i) Total flight time:

To find the total time, we much keep in mind that it is the time that the bill would take to reach the same height level as its starting height, the equation that will be used is as follows:

`\begin{gathered} y(t)=y_o+v_o\sin (\theta)t-(1)/(2)gt^2\Rightarrow(1) \\ y_o=0 \\ v_o=12ms^(-1) \\ g=9.8ms^(-2) \end{gathered}`

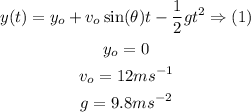
By setting equation (1) equal to zero and solving for the "t" , the total flight time can be solved, it can be done as follows:

`\begin{gathered} y_o+v_o\sin (\theta)t-(1)/(2)gt^2=0 \\ \therefore\rightarrow \\ 0+(12ms^(-2))\sin (50)t-(1)/(2)(9.8ms^(-2))t^2=0 \\ \therefore\rightarrow \\ (12ms^(-2))\sin (50)t=(1)/(2)(9.8ms^(-2))t^2\Rightarrow t=((2)(12ms^(-2))\sin(50))/((9.8ms^(-2))) \\ t=((2)(12ms^(-2))(0.76604444))/((9.8ms^(-2)))=1.8760s \\ t=1.8760 \end{gathered}`

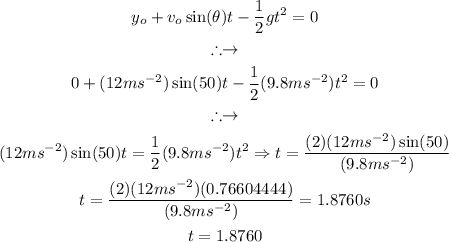
(ii) Maximum height of the ball:

The maximum height that the ball can reach would be attained in half of the total flight time, therefore we need to simply find the y(t) at half of the total flight time, this is done as follows:

`\begin{gathered} t_{h_{}}=(t)/(2)\Rightarrow t_{h_{}}=(1.8760)/(2)=0.938s \\ t_{h_{}}=\text{ }0.938s \\ \therefore\rightarrow \\ y(t_{h_{}}=\text{ }0.938s)=(12ms^(-2))\sin (50)(0.938s)-(1)/(2)(9.8ms^(-2))(0.938s)^2 \\ y(t_{h_{}}=\text{ }0.938s)=(12ms^(-2))(0.76604444)(0.938s)-(1)/(2)(9.8ms^(-2))(0.938s)^2 \\ y(t_{h_{}}=\text{ }0.938s)=8.623-4.5962=4.0268m \\ y(t_{h_{}}=\text{ }0.938s)=h_(\max ) \\ \therefore\rightarrow \\ h_(\max )=4.0268m \end{gathered}`