Question

A small block, with a mass of 4 kg. starts from rest at the top of the apparatus. It then slides without friction down the incline, across the level section on the right. It then colides with a spring and compresses it, which momentarily brings the block to a stop. The maximum height of the incline is 5 m and the spring constant is 120 N/mA.Find the intial potential energy of the block at point AB.Find the velocity of the block at the bottom of the incline at point b C.How much will the block compress the spring before coming at a stop at point b

Answer 1

Given:

The mass of the block, m=4 kg

The initial height of the block, h=5 m

The spring constant of the spring, k=120 N/m

To find:

A. Initial potential energy of the block.

B. Velocity of the block at the bottom of the incline.

C. The compression in the spring.

Step-by-step explanation:

A.

The gravitational potential energy is the energy possessed by an object due to its height.

Thus the initial potential energy of the block is given by,

`PE=mgh`

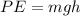
Where g is the acceleration due to gravity.

On substituting the known values,

`\begin{gathered} PE=4*9.8*5 \\ =196\text{ J} \end{gathered}`

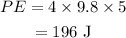
B.

From the law of conservation of energy, the total energy of an isolated system always remains constant. As the block slides down the apparatus, it loses its potential energy. And as there is no friction, the potential energy lost will be converted completely into the kinetic energy of the block.

Thus, when the block is at the bottom of the incline,

`PE=(1)/(2)mv^2`

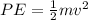
Where v is the velocity of the block when it is at the bottom of the incline.

On substituting the knwon values,

`\begin{gathered} 196=(1)/(2)*4* v^2 \\ \Rightarrow v=\sqrt{(196*2)/(4)} \\ =10\text{ m/s} \end{gathered}`

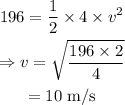
C.

From the law of conservation of energy, the total energy of the system remains the same.

Thus, when the block is stopped, the kinetic energy of the block is completely converted into the elastic potential energy of the spring. Thus the initial potential energy of the block is equal to the spring potential energy stored in the spring when it is compressed and the block is stopped.

Thus,

`PE=(1)/(2)kx^2`

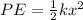
Where x is the compression in the spring.

On substituting the known values,

`\begin{gathered} 196=(1)/(2)*120* x^2 \\ x=\sqrt{(196*2)/(120)} \\ x=1.81\text{ m} \end{gathered}`

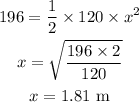
Final answer:

A. The initial potential energy of the block is 196 m

B. The velocity of the block at the bottom of the incline is 10 m/s

C. The compression in the spring 1.81 m