Step 1: Figure of a regular hexagon shown below
Step 1: Determine the length of the side of the hexagon
Let the side of the hexagon = x
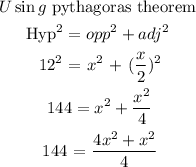
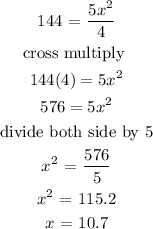
Step 3: Find the Perimeter of the hexagon
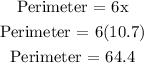
Step 4: Find the Area of the hexagon
![\begin{gathered} A=3\frac{\sqrt[\square]{3}}{2}a \\ A\text{ = 3}\frac{\sqrt[\square]{3}}{2}\text{ (10.7)} \\ \text{A = 27.89} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xe91odzgdspz6pf4mg5qklif274627cfra.png)
Hence the perimeter and area of the hexagon are 64.4 and 27.89