Question

the weight of an ice cream carton are normally distributed with a mean weight of 12 ounces and a standard deviation of 0.4.a. what is the probability that the randomly selected carton has a weight greater than 12.12 ounces b. A sample of 36 carton is randomly selected. what is the probability that their mean weight is greater than 12.12 ouncesround your answers to four decimal places

Answer 1

μ = 12

σ = 0.4

a) P (X > 12.12)

We are given that the distribution of weights of ice cream cartons is a normal distribution. Formula:

`Z\text{ score = }\frac{x\text{ - }\mu\text{ }}{\sigma}`

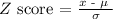
P (X > 12.12) = P (Z > 0.3) = 1 - P(Z ≤ 0.3) = 1 - 0.618 = 0.382

b) P(weight of 36 randomly selected cartons is greater than 12.12 ounces)

Now, as we are working with a sample, the formula will be:

`Z\text{ score = }\frac{x\text{ - }\mu\text{ }}{\frac{\sigma}{\sqrt[]{n}}}`

P (X > 12.12) = P (Z > 1.8) = 1 - P(Z ≤ 1.8) = 1 - 0.964 = 0.036