Question

A)state the domain B)state the rangeC) graph the relation D)is it a function E) is it a one to one function

Answer 1

From the question we are given

`\mleft\lbrace(x,y)\colon|x|+|y|\le2\text{ and }\lvert y\rvert\le1\mright\rbrace`

Graphing the relation we have

From the graph, we have

A. Domain

The domain of the function is

`\lbrack-2,2\rbrack`

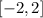
B. Range

The range of the function is

`\lbrack-1,1\rbrack`

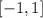
C. The graph of the relation is as shown above

D. From the graph, the relation is not a function.

E. Since the relation is not a function then it is not one-to-one