Question

m varies jointly with x, the cube of y, and the square root of z. m=160 when x=2 y=2 and z=4. Find m when x=3 y=3 and z=49.

Answer 1

Given that:

m varies jointly with x, the cube of y, and the square root of z, The statement means

`m\propto xy^3√(z)`

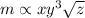
We convert the expression above into an equation by introducing a constant, k,

It becomes

`m=kxy^3√(z)`

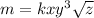
Where

`m=160,\text{ when x}=2,y=2\text{ and z}=4`

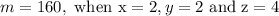
Substitute the values of variables into the equation above to find the constant, k.

`\begin{gathered} m=kxy^3√(z) \\ 160=k(2)(2^3)(√(4)) \\ 160=k(2*8*2) \\ 160=32k \\ Divide\text{ both sides by 32} \\ (32k)/(32)=(160)/(32) \\ k=5 \end{gathered}`

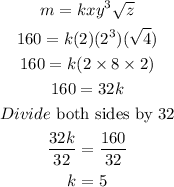
Thus, the equation becomes

`m=5xy^3√(z)`

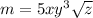
To find the value of m when

`x=3,y=3\text{ and z}=49`

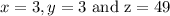
Substitute the values of the variables into the equation above

`\begin{gathered} m=5xy^3√(z) \\ m=5(3)(3^3)(√(49)) \\ m=5(3)(27)(7) \\ m=2835 \end{gathered}`

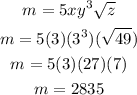
Hence, the value of m is 2835