Answer:

Explanation:
A diameter that is perpendicular to a chord divides the chord into two equal parts.
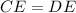
Therefore, if CD=12 and AB=20
The perpendicular bisector of a chord passes through the center of the circle
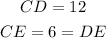
Since AB is the diameter of the circle and O is the center of the circle, AO=10, and OB=10. CO is a radius, then CO=10.
We can use the Pythagorean theorem to find the measure for OE:
![\begin{gathered} OE^2+6^2=10^2 \\ OE=\sqrt[]{10^2-6^2} \\ OE=\sqrt[]{100-36} \\ OE=\sqrt[]{64}=8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dh3uofylnc2i6iu9v0qfmhn1ox78rvxlt2.png)