Question

I need help with part 7 a thru f. Please

Answer 1

Let x be the smallest of the 3 integers, then since the sum of the three consecutive even integers is 6356 we can set the following equation:

`x^2+(x+2)^2+(x+4)^2=6356.^{}`

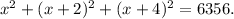
Simplifying the above equation we get:

`\begin{gathered} x^2+x^2+4x+4+x^2+8x+16=6356, \\ 3x^2+12x+20=6356. \end{gathered}`

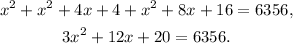
Then to answer this question we must solve the following equation:

`3x^2+12x-6336=0.`

Using the quadratic formula for second-degree equations we get:

`x=\frac{-12\pm\sqrt[]{12^2-4(3)(-6336)}}{2(3)}\text{.}`

Therefore:

`x=44\text{ or x=}-48.`

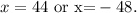
Since the problem is asking for positive integers, then x=44, and the integers are 44, 45, and 46, therefore its sum is 135.

Answer: 135.