(a)
As we can see from the table, each consecutive term is two times the previous value, so we only need to double the value of the previous term.
(b)
From sequence B, we have:
![\begin{gathered} \text{ term number }=0\Rightarrow\text{ value }=2 \\ \text{term number}=1\operatorname{\Rightarrow}\text{value}=12 \\ \text{term number}=2\operatorname{\Rightarrow}\text{value}=22 \\ \text{term number}=3\operatorname{\Rightarrow}\text{value}=32 \\ \text{term number}=4\operatorname{\Rightarrow}\text{value}=42 \end{gathered}]()
Then, we can see that each consecutive term can be calculated if we add 10 units to the previous term.
(c)
Mathematically, this is:
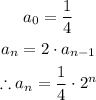
d)
Mathematically, this is:
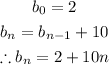
(e)
Now, we evaluate each sequence at n = 9:
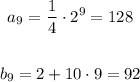
We conclude that A(9) is greater than B(9)