Question

Hi I need to know with equation is a one solution , no solution anf a infinite solution

Answer 1

The equation of a line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Let's write each equation given in the exercise as a System of equations and then let's write each equation in Slope-Intercept form. Then:

Equation 1 as a System of equations

`\begin{cases}y=2(x-1)+6\Rightarrow y=2x-2+6\Rightarrow y=2x+4 \\ y=4x-22\end{cases}`

You can identify that the slope and the y-intercept of the first equation are:

`\begin{gathered} m_1=2_{} \\ b_1=4 \end{gathered}`

And the slope and the y-intercept of the second equation are:

`\begin{gathered} m_2=4 \\ b_2=-22 \end{gathered}`

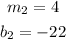
Since:

`\begin{gathered} m_1\\e m_2 \\ b_1\\e b_2 \end{gathered}`

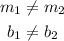
The lines intersect each other and the System of equations has one solution.

Equation 2 as a System of equations

`\begin{cases}y=6(2x+1)-2\Rightarrow y=12x+6-2\Rightarrow y=12x+4 \\ y=12x+4\end{cases}`

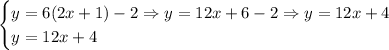
You can see that:

`\begin{gathered} m_1=m_2 \\ b_1=b_2 \end{gathered}`

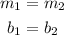
Therefore, since they are the same line, the system has infinite solution​s.

Equation 3 as a System of equations

`\begin{cases}y=2(4-x)\Rightarrow y=-2x+8 \\ y=-2(1+x)-2\Rightarrow y=-2-2x-2\Rightarrow y=-2x-4\end{cases}`

Since:

`\begin{gathered} m_1=m_2 \\ b_1\\e b_2 \end{gathered}`

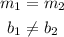
You can determine that the lines are parallel. Therefore, the System of equations has no solution.

The anwer is:

- The first equation has one solution.

- The second equation has infinite solution​s.

- The third equation has no solution.