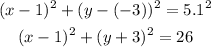Question

for the given circle determine the following:the center, (h,k) is_______.the radius is_______. round to the nearest tenth.the equation of the circle is_______.

Answer 1

Center = (1, -3)

Radius = 5.1

Equation: (x-1)² + (y+3)² = 26

Step-by-step explanation:

Taking into account the figure, we can say that the center of the circle is the point (h, k) = (1, -3)

Then, to calculate the radius of the circle, we need to find the distance between the points (1, -3) and (2, 2).

So, the distance between two points (x1, y1) and (x2, y2) can be calculated as:

`\text{Distance = }\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}`

Replacing (x1, y1) by (1, -3) and (x2, y2) by (2, 2), we get that the distance or radius of the circle is equal to:

`\begin{gathered} \text{Distance = }\sqrt[]{(1-2)^2+(-3-2)^2} \\ \text{Distance}=\sqrt[]{(-1)^2+(-5)^2} \\ \text{Distance = }\sqrt[]{1+25} \\ \text{Distance = }\sqrt[]{26}=5.1 \end{gathered}`

So, the radius of the circle is 5.1

Finally, the equation of a circle is:

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) is the center and r is the radius. So, replacing (h, k) by (1, -3) and r by 5.1, we get that the equation of the circle is:

`\begin{gathered} (x-1)^2+(y-(-3))^2=5.1^2 \\ (x-1)^2+(y+3)^2=26 \end{gathered}`