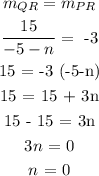Answer:
n = 0
Explanations:
Points are collinear if they are lying on the same line.
For three points to be collinear, the slopes of any two points on the line must be equal.
This means that the slope of PQ must be equal to the slope of QR and the slope of PR
The slope of a line joining two points is given by the formula:
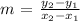
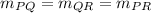
For the point P(3, -11), Q(n, -2)
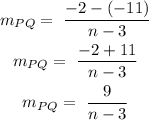
For the points Q(n, -2), R(-5, 13)
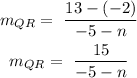
For the points P(3, -11), R(-5, 13):

Since the slopes of any two points on the three collinear points must be equal: