Let's make a diagram to visualize the problem.
In this situation, the initial vertical speed is null because the given speed is a horizontal component. To find the time spent in the air, we can use the following formula.
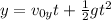
Where the initial speed is null, the acceleration is gravity, and y is the height of the table.
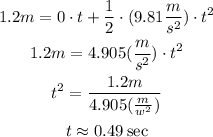
(a) Therefore, the ball spent 0.49 seconds in the air before hitting the ground.
To find the maximum horizontal range x, we have to use the following formula.
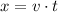
Where v = 2.5 m/s and t = 0.49 seconds. Let's use these values to find x.
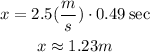
(b) Therefore, the maximum horizontal range is 1.23 meters.
At last, we have to use a triple-speed to find the answer to c.
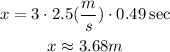
(c) Therefore, the ball will land 3.68 meters away from the table.