SOLUTION
16A. We want to find the relationship between n and 4 in
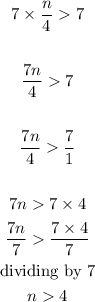
Therefore, the relationship between n and 4 is that n must be greater than 4
16B. The relationship between a and b
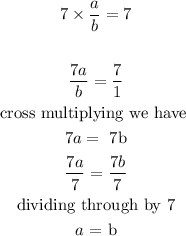
Therefore the relationship between a and b is that a must be equal to b
a = b