Question

**Convert to vertex form & describe thetransformations of the following functionfrom y = x2 - 2x + 3 = 0

Answer 1

Explanation:

To convert the equation in standard form to vertex form, you have to use the completing square method:

`y=x^2-2x+3`

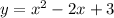
Extract a from the first two terms:

`y=a\cdot(x^2+(b)/(a)\cdot x)+c`

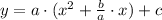
Complete the square for the expressions with x. The missing fraction is (b/(2a))². Add and subtract this term in the parabola equation

`\begin{gathered} y=a\cdot\mleft[x^2+(b)/(a)\cdot x+b/\mleft(2a\mright)^2-b/\mleft(2a\mright)^2\mright]+c \\ \text{Simplifying;} \\ y=a\cdot\mleft[\mleft(x+(b)/(2a)\mright)^2-b/\mleft(2a\mright)^2\mright]+c \end{gathered}`

Substitute the a,b and c terms respectively:

`\begin{gathered} y=a\cdot\mleft[x^2+(b)/(a)\cdot x+b/\mleft(2a\mright)^2-b/\mleft(2a\mright)^2\mright]+c \\ \text{Simplifying;} \\ y=a\cdot\mleft[\mleft(x+(b)/(2a)\mright)^2-b/\mleft(2a\mright)^2\mright]+c \end{gathered}`