ANSWER :
x > 2
EXPLANATION :
From the problem, we have the inequality :
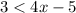
Solve for x :
Put the terms with variables on the left side and the constants to the right side.
Subtract 4x from both sides :
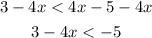
Subtract 3 from both sides :
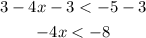
Divide both sides by -4.
Take note that if you divide a negative number from the inequality, the symbol will change.
So from "<", it will become ">"

The solution is x > 2
The graph will be :
The boundary line is a dashed type since the symbol is ">" and the region is to the right of x = 2